In silico Evaluation of Crosslinking Effects on Denaturant meq values and ΔCp upon Protein Unfolding
-
Hamzeh-Mivehroud, Maryam
-
Biotechnology Research Center, Tabriz University of Medical Sciences, Daneshgah Street, Tabriz, Iran
-
Alizade, Ali Akbar
-
Biotechnology Research Center, Tabriz University of Medical Sciences, Daneshgah Street, Tabriz, Iran
-
School of Pharmacy, Tabriz University of Medical Sciences, Tabriz, Iran
-
Ahmadifar, Monire
-
Biotechnology Research Center, Tabriz University of Medical Sciences, Daneshgah Street, Tabriz, Iran
-
School of Pharmacy, Tabriz University of Medical Sciences, Tabriz, Iran
-
 Dastmalchi, Siavoush
Siavoush Dastmalchi, Ph.D., Department of Medicinal Chemistry, School of Pharmacy, Tabriz University of Medical Sciences, Tabriz, Iran , Tel: +98 411 3364038 Fax: +98 411 3379420 E-mail: dastmalchi.s@tbzmed.ac.ir
Dastmalchi, Siavoush
Siavoush Dastmalchi, Ph.D., Department of Medicinal Chemistry, School of Pharmacy, Tabriz University of Medical Sciences, Tabriz, Iran , Tel: +98 411 3364038 Fax: +98 411 3379420 E-mail: dastmalchi.s@tbzmed.ac.ir
-
Biotechnology Research Center, Tabriz University of Medical Sciences, Daneshgah Street, Tabriz, Iran
-
School of Pharmacy, Tabriz University of Medical Sciences, Tabriz, Iran
Abstract: Important thermodynamic parameters including denaturant equilibrium m values (meq) and heat capacity changes (ΔCp) can be predicted based on changes in Solvent Accessible Surface Area (SASA) upon unfolding. Crosslinks such as disulfide bonds influence the stability of the proteins by decreasing the entropy gain as well as reduction of SASA of unfolded state. The aim of the study was to develop mathematical models to predict the effect of crosslinks on ΔSASA and ultimately on meq and ΔCp based on in silico methods. Changes of SASA upon computationally simulated unfolding were calculated for a set of 45 proteins with known meq and ΔCp values and the effect of crosslinks on ΔSASA of unfolding was investigated. The results were used to predict the meq of denaturation for guanidine hydrochloride and urea, as well as ΔCp for the studied proteins with overall error of 20%, 31% and 17%, re-spectively. The results of the current study were in close agreement with those obtained from the previous studies.
Introduction :
Through the human genome project we now know that a human cell can synthesize about 20,000 to 25,000 different proteins (1). Proteins are an important class of biological macromolecules present in all biological or-ganisms, and constitute high proportion of the dry mass of all cells (2). Most of the biological processes in all cells are executed by proteins. The amino acid sequence of a protein contains all information needed for adopting its three-dimensional structure. However, misfolding does occur, even though help from other mo-lecules, such as chaperons, for correct and fast in vivo folding are in place (3-5).
Denaturation studies are very useful for in-vestigating the thermodynamic properties of proteins. Transition from native to denatured states can be brought about by changing the properties of protein's environment. In gen-eral, this can be done by increasing the tem-perature, adding chemical denaturants or changing the pH.
Urea and guanidinium ion (used in the form of guanidinium chloride-GdnHCI) favor the denatured state by increasing the solubility of the unfolded chain in an aqueous solution. In comparison to temperature denaturation, che-mical denaturation is often a reversible pro-cess. This is possible since the hydrophobic groups of the unfolded chain are shielded by the denaturants, which prevent aggregation.
The unfolding free energy (ΔGU) depends
linearly on the denaturant concentration as:
Where is the free energy of un-folding in the absence of denaturant and mU denotes the dependency of free energy on de-naturant concentration (i.e. meq) (6). A good linearity is observed at high denaturant con-centrations and is obtained by extra-polation to the zero concentration of denatur-ant. values calculated from guanidin-ium chloride and urea denaturation are in very good agreement (7) which gives this relation some further credibility.
One of the major challenges in the field of protein science is to predict the stability and function of proteins from their primary struc-tures. To accomplish this task, efficient algo-rithms are needed to relate the structure to sta-bility. The availability of about 77,000 protein structures in Protein Data Bank (PDB) (8) and a great deal of experimental works on the thermodynamic stability of proteins have provided a wealth of information which can be used for the development of empirical functions that relate thermodynamic and structural parameters.
The success of such approach in developing structure-based methods to predict various thermodynamic parameters that define the Gibbs energy, i.e., the enthalpy, entropy and heat capacity changes, has been shown previ-ously (9-13). In the process of unfolding, the major contribution to the enthalpy change arises from the disruption of intramolecular interactions such as van der Waals and hydro-gen bonds and also solvation of the interact-ing groups. Therefore, the change in solvent accessible surface area (ΔSASA) upon unfold-ing has been used as a mean for predicting the ΔH as presented below:
Where ΔSASAi is the change in SASA of atom i upon unfolding, and is a coef-ficient that depends on the atom type and the average packing density of that atom within the protein (14).
The heat capacity change (ΔCp) in protein unfolding largely arises from changes in the hydration of groups that are buried in the native form away from the surrounding aque-ous environment. ΔCp is correlated to the changes in SASA upon unfolding, as shown in the following equation:
Where ai is the contribution of atom i per unit area and ΔSASAi is as defined above. Using both equations, good correlations were obtained between experimental and calculated ΔH and ΔCp values (14).
The aim of current study is to develop em-pirical models to account for the effect of crosslinks on ΔSASA and hence on thermody-namic parameters (i.e., meq and ΔCp) of protein unfolding based on computational approach.
Materials and Methods :
Databases and programs
The experimental meq values for urea and GdnHCl denaturation, as well as ΔCp dena-turations for a set of 45 proteins used in this study were from Myers et al (10). The three-di-mensional (3D) structures of the studied pro-teins were obtained from Protein Data Bank (http://www.rcsb.org/) at RCSB (8).
The SASA of the proteins in folded and un-folded forms were calculated using DSSP program implemented in GROMACS pack-age. The DSSP program was designed by Wolfgang Kabsch and Chris Sander to stand-ardize secondary structure assignment based on a database of secondary structure for pro-tein entries in the PDB (15).
Swiss-Pdb Viewer (SPDBV, version 3.7, Swiss Institute of Bioinformatics), an inter-active molecular graphics program was used for viewing and analyzing protein structures (16). HyperChem (version 7.1; 2002; Hyper-cube Inc.) is the other molecular modeling software used in this study.
GROMACS (version 3.3, University of Groningen, The Netherlands, currently main-tained by ScalaLife), an engine to perform molecular dynamics simulations and energy minimization (17) was used under Linux oper-ating system (Fedora core 5) on a cluster con-sisting of 8 nodes each with two dual-core Opteron 2212 CPUs and 2 GB RAM.
Unfolding the proteins
The unfolded states of the proteins were achieved by three different approaches; (i) building the fully extended conformation of the protein, (ii) instantaneously assigning standard bond lengths, bond angles, torsion angles, and stereochemistry properties to the model structure using a given force field method, or (iii) molecular dynamics simu-lation.
Fully extended conformation
SPDBV was used to upload the sequence of the protein saved in FASTA format. Then the sequence was folded into an extended confor-mation by setting phi (φ) and psi (ψ) angles to those corresponding with β-pleated strand. It is clear that in such a conformation there is no crosslink in the generated model even if the native form of protein consists such con-straints.
Instantaneous unfolding using standard bond and angle assignment
HyperChem program was used to open the crystal structure (native form) of protein. In this way, the disulfide bonds are lost. If the re-establishment of crosslinks was desired, first the residues involved in the crosslink were selected and then the necessary bonds were created between the sulfur atoms in-volved in the disulfide bonds. Subsequently, the structure was forced to unfold into a ran-dom coil losing its regular structures while preserving the crosslinks. The unfolded struc-tural model was energy minimized using the molecular mechanics force field.
The minimization protocol employed the steepest descent method using BIO+, the HyperChem implementation of CHARMM (Chemistry at HARvard using Molecular Mechanics) force field (18), until the difference in energy after two consecutive iterations was less than 0.1 kcal/mol. The model structures were stored as unfolded states and their SASA were calculated as described above. In the case of heme containing proteins, two bonds were built linking the chelating atoms to the central iron atom. This effectively constrains the spatial distance between two residues to which the iron atom of the heme group is linked through coordination of the unpaired electrons of nitrogen or sulfur atoms.
Unfolding using molecular dynamics simulation
In order to unfold proteins using Molecular Dynamics (MD) simulation technique, the following steps were performed. First, the native structure was downloaded from PDB at RCSB and converted into standard Gromacs file format. The positions of all hydrogen atoms were reconstructed. Subsequently, the protein structure was energy minimized in vacuum using steepest descent algorithm until the maximum force was smaller than 1.0 kJ mol-1nm-1.
GROMOS-96, the officially distributed force field for Gromacs, was used for molecu-lar mechanics simulations as implemented in the software package (19). Then a simulation box was created and protein was centred into it. The simulation box was filled in by Simple Point Charge (spc216) water and urea mo-lecules. The final concentration of the urea in the box was about 4.4 M. Before running the MD simulation, the system was neutralized by adding appropriate number of either Na+ or Cl– counter ions to have zero net charge. Ultimately, the solvated protein was subjected to MD simulation for 10 ns at 500˚K and the trajectories were saved every 0.02 ns.
Crosslinking factor (CLF)
In order to investigate the effect of cross-linking on the unfolding behaviour of a pro-tein, an index named Crosslinking Factor (CLF) was defined as follows:
Where SASA refers to solvent accessible surface area of unfolded conformation and the subscripts c and nc denote whether the cross-links are preserved or not in the unfolded con-formation, respectively. The value of n equals the number of crosslinks present in any of those proteins studied here which have cross-links in the native form. N is the number of proteins with crosslinks, and i denotes any of the studied proteins used to derive CLF value.
Statistical treatment
Validation of models: Statistical analyses were performed by SPSS (SPSS for windows version 11.5, IBM) and Excel (Microsoft Office 2007) programs. Predictive power of the mathematical models were evaluated by excluding one of the data points, i.e. one of the proteins from the data set of 45 proteins listed in table 1, and training the model based on the remaining proteins and subsequently predicting the value of thermodynamic para-meter for the excluded protein. This was con-tinued until all proteins were used for the pre-diction.
The Standard Deviation of Error of Pre-diction (SDEP) was calculated to give a measure for the distribution of the errors in-volved in the predictions using the following equation:
Here Aexp and Acalc are predicted values, respectively. N denotes the number of data points.
Mean absolute percentage error (MAPE)
To evaluate the accuracy of predictions, ab-solute percentage errors were calculated based on the following equations:
Where Acalc and Aexp are the calculated and experimental values for a given parameter of interest, such as ∆Cp, meq for GdnHCl or urea. The average of APE over all data points for each of the above mentioned parameters was calculated and called MAPE.
Where N is the number of data points.
Results and Discussion :
The changes in solvent accessible surface area (∆SASA) upon unfolding, as determined by the differences in solvent accessibilities of native form (calculated from the crystal struc-ture) and denatured form (modeled by an ex-tended polypeptide chain) are given for a set of 45 proteins in table 1. The table also shows meq values from denaturation experiments, ΔCp of unfolding, number of residues as well as crosslinks present in each of these proteins taken from the compilation made by Myers et al (10).
Figures 1A and 1B demonstrate depend-encies that exist between the denaturants meq values and the changes in the solvent acces-sible surface area upon unfolding. There are significant linear correlations in both cases, with the correlation coefficient (R) values of 0.85 and 0.87 for GdnHCl and urea, respect-ively. The slopes of the linear regression lines are 0.25 and 0.17 cal/ (mol.M.Å2) for GdnHCl and urea, respectively, indicating the stronger denaturing effects of GdnHCl.
Denaturation heat capacity changes (∆Cp) were also correlated with the ∆SASA strongly with the correlation coefficient of 0.97 as shown in figure 1C. The same linear correl-ations between meq values and ∆SASA have been shown previously by Myers et al (10). ∆SASA has been also related linearly to ∆Cp by others (20,21).
The main purpose of this study is to re- evaluate the effect of crosslinks on ∆SASA and also predict the meq and ∆Cp of unfold-ing based on protein sequence information. These latter two parameters are amongst the important criterion indicative of the stability of proteins. Therefore, prediction or any im-provement in the prediction of these values has significant theoretical and practical appli-cations.
The presence of crosslinks such as disulfide bonds and heme groups in a protein (as shown in table 2) will result in a more compact un-folded state, thus reducing the solvent accessi-bility of the unfolded polypeptide chain. To compensate for the effects of crosslinks, Myers et al (10) employed the results of dif-ferent empirical methods (22) to estimate the magnitude of the reduction of solvent acces-sible surface area (∆SASA) per disulfide bond. The reduction of ∆SASA per crosslink was estimated to be about 900Å2.
In the current study, to find out more about the effect of crosslinking through theoretical and computational methods, the different un-folded models were generated for crosslink-containing proteins while the crosslinks were preserved or removed in the unfolded states generated by instantaneous unfolding method based on assigning standard bond length and angle values. Then the SASA values were cal-culated for the generated unfolded structural models (Table 2).
To quantitatively indicate the effect of crosslinks on ∆SASA upon unfolding a new term called Crosslinking Factor (CLF) was in-troduced (CLF was described in Materials and Methods section.) Effectively, CLF is a meas-ure of reduction in the SASA of unfolded pro-tein as a consequence of presence of a single crosslink, such as disulfide bond, and calcu-lated to be equal to 918.5 Å2. This value is the average of crosslinking numbers calculated for 16 crosslink-containing proteins listed in table 2 for which the meq and ∆Cp values were available.
In five proteins listed in the table, cross-links are formed via ligation of central ion atom of heme groups by sulfur or nitrogen atoms of the side chains of the interacting re-sidues. The average of crosslinking numbers for these proteins (759.0 Å2) is smaller than the average of the numbers (991.0 Å2) for the remaining proteins where the crosslinks are formed by disulfide bounds. However, the difference is not statistically significant (p-value >0.05). None of these values are stat-istically different from the calculated CLF value of 918.5.
Based on the above findings, the ∆SASA values were corrected for the effect of cross-links on the solvent accessibility of the un-folded state by taking 918.5 Å2 per crosslink off the ΔSASA (called ΔSASAcorrected) and then the corrected values were re-correlated to the meq and ∆Cp values. Linear correlation coef-ficients improved to 0.90, 0.88 and 0.99 for GdnHCL and urea meq as well as ∆Cp values, respectively as shown in figure 2.
The extent of increase in SASA upon un-folding of a protein highly depends on the number of residues (i.e. protein size) and the constraints present in the unfolded state. The unfolded state of a protein is populated by an ensemble consisting huge number of con-formationally distinct species. The presence of structural constraints limits the conform-ational space available to be explored by the protein polypeptide chain. Our analyses, in agreement with the results of others (10), show that the amount of area buried in each protein correlates very strongly (R=0.99) with the number of residues in each protein (Eq. 9). The strong correlation between ∆SASA and the number of residues, makes it possible to estimate the thermodynamic parameters using equations 10 to 12.
Where k denotes the number of residues for a given protein. These equations provide means to predict meq and ΔCp directly based on the primary structure information. The re-sults of experimental studies are in close agreement with the results of our theoretical calculations which indicate the important thermodynamic parameters can be predicted using ∆SASA upon unfolding and taking into account the presence of crosslinks in the pro-tein.
In a different approach to estimate SASA of unfolded state of proteins, we have used MD to simulate the unfolding behavior of proteins in denaturing condition, as stated in Materials and Methods section. Four of the proteins in our dataset (listed in Table 3) were subjected to MD simulations for 10 ns at 500 ºK while inserted in a solvation box filled by a mixture of water and urea molecules. As can be seen from the table, the maximum SASA values for the unfolded conformations of proteins ob-tained by MD are smaller than that achieved by non-simulation method. Consequently, the ΔSASA values are also relatively smaller.
Figure 3 shows the snapshots of conform-ational changes during unfolding simulation of IgG binding domain of protein G (IBPG) which has 56 residues with no crosslink. As time evolves, both tertiary and secondary structures of IBPG are lost and at the same time its SASA increases. The maximum SASA achieved during 10 ns is 5772 Å2 which is less than that estimated for fully extended con-formation (8143 Å2).
The presence of crosslinks in the unfolded state will result in a more compact unfolded form and the higher the number of crosslinks, the more pronounced is this effect. For ex-ample, as shown in figure 4, the unfolded conformation of lysozyme (hen egg white), a 129-residue protein with four disulfide bonds, retained more globular shape at the end of MD simulation, although it loses the elements of secondary structures.
As shown in table 3, the SASAs of the investigated proteins increased at the end of MD simulation. However, the extent of this increase is bigger for the protein with no crosslink. For example 1PGB which is a 56-residue protein without any crosslink showed 54% increase in SASA upon unfolding using MD method. However, applying the same un-folding condition on 1AAL, a protein with al-most equal size (i.e. 58 residues) and two disulfide bond has led to only 40% increase in SASA. In all studied cases, the maximum SASA for unfolded conformations achieved by MD are smaller than that of instantaneous method.
Analyses of MD trajectories showed that the RMSD differences for C atoms increases as time evolves approaching high values in the range of ~14-19 Å for the studied proteins during the simulation. The rate of RMSD in-crease was dramatically fast for 1PGB and 2TRX, with no and one crosslink, respective-ly. However, the rate was gradual in the case of 1AAl and 1AKI with two and four cross-links, respectively.
Although MD simulation under the condi-tion used in this study can unfold the proteins and also demonstrates the effect of crosslink, however, using this method the SASA of un-folded conformations never reached to the SASA values of the unfolded conformations obtained by instantaneously decomposing the protein native structure just by taking into consideration to preserve the standard bond lengths, bond angles and other standard chem-ical structure geometries. This could be due to insufficient simulation time or entrapment of protein in an ensemble of conformations in a local minimum of energy landscape. How- ever, to find out more about these issues and draw more sensible conclusion, further com-putational experiments such as hydrodynamic simulation are required.
Crosslinks such as disulfide bonds and heme groups have profound effect on the con-formational flexibility and SASA values of un-folded state and hence influence the stability of the proteins by decreasing the entropy gain as well as reduction of ΔSASA upon unfold-ing. Studies of proteins with chemical cross-links have shown clearly that the major effect of the crosslink on the stability results from a decrease in the conformational entropy of the unfolded molecule (23,24).
On the other hand, attempts to increase the stability of proteins through introducing disul-fide bonds suggest that the structural re-straints in the native state due to the cross-links may also make an important contribu-tion to the net effect of the crosslinks on the stability (25). Furthermore, inspection of the model structures of Micro-myoglobin (Mb) revealed a role for heme in stabilizing the folded state (26).
Doig and Williams (27) investigated the ef-fect of disulfide crosslinks on hydrophobicity derived stability of proteins. Based on data obtained from solvent transfer experiment, they calculated the non-polar ∆SASA to be 590 and 690 Å2 per disulfide bond according to free energy of hydration and ∆Cp measure- ments, respectively. Taking into account that the fraction of total area buried which is non-polar is about 0.70, these values correspond to a reduction in the total area change of 850 Å2 and 990 Å2 per disulfide. Using solvent per-turbation difference spectroscopy, Pace et al demonstrated that the solvent accessibility of the aromatic residues (Tyr and Trp) in three studied proteins (lysozyme, RNase A and RNase T1) was changed upon unfolding (22). Myers et al, used these experimental data to estimate an approximate average value of 900 Å2 reduction in ∆SASAunfolded per disulfide, as-suming a universal change in accessibility across all residue types (10).
The results of these experimental methods have been averaged and used by Myers et al to compensate for the effects of crosslinks on ΔSASA. However, it may suffer from an over simplification by using only the changes in accessibility of just two amino acids and ex-trapolating these changes to the total area. It should also be mentioned that these results have been concluded from very limited num-ber of experiments performed on only three globular proteins (22).
One of the shortcomings of using either CLF, introduced in this work, or experimen-tally derived value of 900, introduced by Myers et al to compensate for the effects of crosslinks on ΔSASA and hence estimation of meq and ΔCp values is the scarcity of the data used. The correction value close to 900 Å2 (proposed by Myers and here as CLF) can be justified by fitting equations 12 to 14 pre-sented in Myers et al where the disulfide bond corrections that maximize the fits are all close to 900 Å2. However, there is no need to use a correction factors such as 900 Å2 proposed by Myers or CLF to account for the effects of crosslinks on meq or ΔCp. Although we be-lieve the correction factor most likely is close to 900 Å2, but it is not a magic number and any other value close to that can be used to do the correction and then draw empirical equa-tions to relate meq or ΔCp to the corrected ΔSASA (or to the combination of number of amino acids and CLF as we used in here).
The coefficients in the final mathematical equations will be adjusted to balance out any changes in the value of correction factor. In a situation where the ultimate aim is to be able to predict the thermodynamic parameters as precise as possible, one may decide to use dif-ferent structural descriptors to derive empir-ical equations for the prediction purposes.
To this end we have furthered our investi-gation by trying to develop different empirical equations to predict meq and ΔCp values. We have examined the effects of different struc-tural properties such as number of amino acids, number of crosslinks, size of loops re-presenting the total number of amino acids involved in the loops formed by crosslinks, and the central position of the regions in the loop area on the prediction of the thermo-dynamic properties. The best statistical Mul-tiple Linear Regression (MLR) models were achieved using variables representing total number of amino acids and the number of crosslinks.
In order to test the predictive power of these models, the Leave One Out (LOO) cross validation method was used. The mean ab-solute percentage error of predictions (MAPE) of meq(GdnHcl), meq(Urea) and ΔCp values for all proteins listed in table 1 (or proteins with crosslinks listed in table 4) based on Myers’ models are 19.7 (21.5), 22.9 (31.8) and 13.8 (17.9). The corresponding MAPEs using models presented in equations 13, 14 and 15 are 22.3 (20.5), 23.6 (31.1) and 13.5 (16.8), respectively.
The results show that both methods are not statistically different in predicting the evalu-ated thermodynamic parameters, either for all data points (proteins in Table 1) or for the proteins with crosslinks (i.e. values indicated inside the brackets), and simple MLR equa-tions based on limited number of structural descriptors, i.e. number of residues and num-ber of crosslinks, are able to perform equally well. In fact equations 13 to 15 are identical to equations 10 to 12 and the only difference is the way to represent the effect of crosslink on the parameter of interest. For example in equation 13 the coefficient of variable n (i.e. number of crosslinks) equals to the coefficient of the second term on the right hand side of the equation 10 multiplied by the value of CLF. These equations are also too close to the equations proposed by Myers et al (eqs. 12 to 14 in reference 10). For instance, the coef-ficient of variable n in equation 14 above (i.e. 155.58) is very close to the 139.3 calculated by multiplying 0.14 and 995 in equation 13 in Myers’ study (10).
Conclusion :
In summary, it can be concluded that the proposed relationships represent valuable tools for predicting thermodynamic para-meters of protein folding using the primary sequence information. The proposed cross-linking factor (CLF; which shows the effect of a single crosslink on ΔSASA upon unfold-ing) of 918.5 Å2 obtained based on com-putational simulation is very close to the pre-viously published experimentally derived value of 900 Å2. Such a correction factor can be used to estimate the ΔSASA upon unfolding which in turn can be used for the prediction of thermodynamic parameters such as meq and ΔCp. For the prediction of these parameters, one may also use number of amino acids (k) and number of crosslinks (n) without need to any kind of correction factor.
Although the correction factor for the effect of crosslink on ΔSASA is a quantitative value describing a fundamental property in protein folding, however, for the prediction purposes, the use of more simple properties taken from the primary structure of proteins gives as well accurate results. In addition, the current work demonstrates an example where theory is cap-able of reproducing the results obtained from experimental works.
Acknowledgement :
Authors would like to thank Research Of-fice of Tabriz University of Medical Sciences and Iran National Science Foundation for pro-viding financial support.

Figure 1. Dependence of A) meq value for Gdn HCl denaturation, B) meq value for urea denaturation, and C) heat capacity changes upon unfolding on ∆SASA for the 45 proteins shown in table 1
|
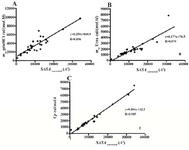
Figure 2. Dependence of A) meq value for GdnHCI denaturation, B) meq value for urea denaturation, and C) heat capacity changes upon unfolding on ∆SASA after correction for the effect of crosslinks by taking out 918.5 Å2 per crosslink for the 45 proteins in our data set (see text for further explanation)
|
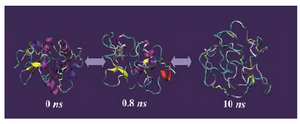
Figure 3. Molecular dynamics simulation of IgG binding domain of protein G (PDB code 1PGB) solvated in 4.4 M urea in water at 500 ºK for 10 ns using GROMOS-96 force field parameters. The non-protein molecules (i.e. water and urea) are not shown for the sake of clarity
|
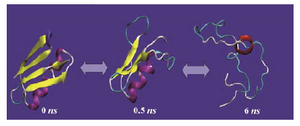
Figure 4. Molecular dynamics simulation of lysozyme (hen egg white) (PDB code 1AKI) solvated in 4.4 M urea in water at 500 ºK for 10 ns using GROMOS-96 force field parameters
|

Table 1. Characteristics of 45 proteins that have meq values and crystal structures available a.
NA: Not Available; a for each protein, the PDB file code, number of residues, and number of disulfides or covalent heme-protein crosslinks is shown. SASA values were calculated by DSSP program as described in the text. The 5, 6 and 7th columns give experimental meq values for GdnHCI or urea denaturation and the observed ∆Cp, for each protein, taken from reference (10). ∆SASA values are in Å2, meq values in cal/(mol.M), and ∆Cp, in cal/(mol.K); b SASAunfolded values in this table were calculated using the extended -strand conformation of all proteins; c Dimer; dThese values were checked and corrected based on the number of the residues in the corresponding PDB files and hence are different from those reported in Myers et al. (10).
|
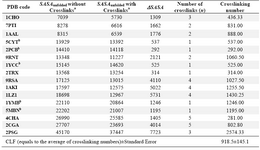
Table 2. List of crosslink-containing proteins used in this study. Differences of SASA values for the unfolded stats in two different forms, i.e., with and without conserving the crosslinks, have been shown along with the number of crosslinks and crosslinking number for each protein
a In order to be consistent, the results presented in this table were derived from instantaneous unfolding method using standard bond length and angle values for both sets of data labeled "without crosslinks" and "with crosslinks" and then the SASA values were calculated using DSSP. b The heme containing proteins
|
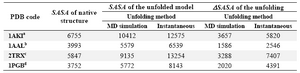
Table 3. Comparison of SASA and SASA values obtained by different methods used to unfold the proteins
a, b, c and d are 4, 2, 1, and zero, respectively and denote the number of crosslinks
|
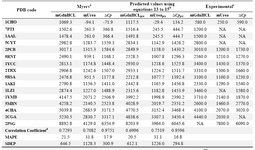
Table 4. Thermodynamic parameters of proteins predicted based on different methods
a: Prediction of heat capacity changes and meq values for GdnHCL and Urea upon unfolding based on Myers� equations (10). b: Same predictions using equations 13-15. c: Experimental data which are compiled from the literature and taken from reference (10). d: Correlation coefficient between predicted and experimental values
|
|